Mathematical and Numerical Analysis of Nonlocal PDE models
Nonlocal partial differential equations (PDEs) trace their origins to the exploration of physical phenomena featuring nonlocal interactions or extended dependencies. In contrast to classical PDEs governing localized interactions, nonlocal PDEs introduce operators considering interactions across distances.
These equations find significance in diverse scientific domains, encompassing physics, biology, finance, and image processing, offering a more accurate depiction of systems where distant interactions are pivotal. They prove essential in capturing phenomena like long-range diffusion, anomalous transport, and spatial patterns that classical PDEs may overlook. Concurrently, fractional PDEs, a niche within nonlocal PDEs, involve fractional derivatives, extending differentiation to non-integer orders. This specialized intersection enables modeling of processes with memory effects and long-range interactions, contributing to a profound comprehension of nonlocal behaviors in scientific and engineering applications.
Our research group at Karlstad University primarily focuses on the following tasks:
1) Mathematical modelling of nonlocal interactions in fields like biology, ecology and game theory
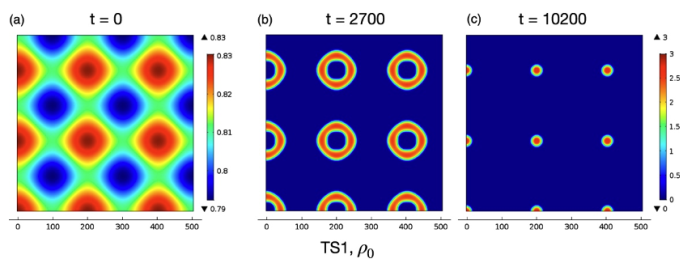
2) Analytical and numerical investigation of pattern formation and blow-u/quenching behaviour of nonlocal systems arising in biology, ecology and industry.
Research Group Members: Associate Professor Nikos I. Kavallaris, Professor Adrian Muntean
Please see also the following link for an upcoming event on Nonlocal PDEs co-organized by our group in Karlstad University